貌似今天是祖冲之诞辰1580周年,Google推出了纪念LOGO,据说这也是Google第一个中国人形象的doodle,看来祖冲之还是很有面子的。
不过,有点纳闷的是,虽然Google用圆代替了其中一个O,而且在下方写下了π=355/113的公式,不禁想问,祖冲之会希腊字母吗?
显然,这个纪念doodle仅仅是展示了“圆周率”这个东西,而对于祖冲之来讲,仅仅能从355/113这个公式中了解出来,而如果不是用Google搜索了一下,我都不知道原来355/113是祖冲之算出来的圆周率的密率。
维基百科关于圆周率:
由于π的超越性,所以只能以近似值的方法计算π。对于一般应用3.14或
已足够,但工程学常利用3.1416(5位有效数字)或3.14159(6位有效数字)。至于密率
则是一个易于记忆(三个连续奇数:113355),且精确至7位有效数字的分数近似值。
[编辑] 实验时期
中国古籍云:“周三径一”[2],意即取 π=3。西元前17世纪的埃及古籍《阿美斯纸草书》(Ahmes,又称“阿梅斯草片文书”;为英国人Alexander Henry Rhind(莱茵德)于1858年发现,因此还称“莱茵德纸草书” Rhind Papyrus)是世界上最早给出圆周率的超过十分位的近似值,为 256/81 ( = 3 + 1/9 + 1/27 + 1/81) 或 3.160。
至阿基米德之前,π值之测定倚靠实物测量。
[编辑] 几何法时期——反复割圆
阿基米德用正96边形割圆术得出圆周率介乎
与
之间。
西元263年,中国数学家刘徽用“割圆术”计算圆周率,他先从圆内接正六边形,逐次分割为12、24、48、96、192边形。他说“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣。”(分割愈精细,误差愈少。分割之后再分割,直到不能再分割为止,它就会与圆周完全重叠,就不会有误差了),其中有求极限的思想。刘徽给出π=3.141024的圆周率近似值,并以
(徽率)为其分数近似值。
西元466年,中国数学家祖冲之将圆周率算到小数点后7位的精确度,这一纪录在世界上保持了一千年之久。同时,祖冲之给出了
(密率)这个很好的分数近似值,它是分母小于10,000的简单分数中最接近π的。为纪念祖冲之对圆周率发展的贡献,日本数学家三上义夫将这一推算值命名为“祖冲之圆周率”,简称“祖率”。可惜祖冲之的著作《缀术》已经亡佚,后人无从得知祖冲之如何估算圆周率的值。
钱大昕的《十驾斋养新录》卷第十七首条〈圆径周率〉引《隋书律历志》:“古之九数,圆周率三圆径率一,其术疏舛,自刘歆、张衡、刘徽、王蕃、皮延宗之徒,各设新率,未臻折衷。宋末南徐州从事史祖冲之更开密率,以圆径一亿为一丈,圆周盈数三(刻本作二,误)丈一尺四寸一分五厘九毫二秒七忽,朒数三丈一尺四寸一分五厘九毫二秒六忽,正数在盈朒二限之间,密率圆径一百一十三,圆周三百五十五,约率圆径七,周二十二。又设开差幂、开差立,兼以正圆参之,指要精密,算氏之最者也。”
[编辑] 分析法时期——无穷级数
这一时期人们开始摆脱利用割圆术的繁复计算,开始利用无穷级数或无穷连乘积求π。
Ludolph van Ceulen(约1600年)计算出π的小数点后首35位。他对此感到自豪,因而命人把它刻在自己的墓碑上。
斯洛文尼亚数学家Jurij Vega于1789年得出π的小数点后首140位,其中有137位是正确的。这个世界纪录维持了五十年。他利用了John Machin于1706年提出的数式。
所有以上的方法都不能快速算出π。第一个快速算法由 Machin 提出:
其中arctan(x) 可由泰勒级数算出。类似方法称为“类Machin算法”。
[编辑] 计算器时代
上万位以上的小数位值通常利用Gauss-Legendre算法或Borweins算法;另外以往亦曾使用于1976年发现的 Salamin-Brent算法。
第一个π和 1/π的小数点后首一百万位利用了古腾堡计划。最新纪录是2002年九月得出的 1,241,100,000,000 个小数位,由拥有1TB主内存的64-node日立超级电脑,以每秒200亿运算速度得出,比旧纪录多算出一倍(206亿小数位)。此纪录由以下类Machin算法得出:
(K. Takano, 1982年)
(F. C. W. Störmer, 1896年)
这么多的小数位没什么实用价值,只用以测试超级电脑。
1996年,David H. Bailey、Peter Borwein及西蒙•普劳夫发现了π的其中一个无穷级数:
以上述公式可以计算π的第n个二进制或十六进制小数,而不需先计算首n-1 个小数位。此类π算法称为Bailey-Borwein-Plouffe算法。请参考 Bailey’s website 上相关程式。
Fabrice Bellard于1997年给出了计算机效率上高出上式47%的BBP算法:
请参考 Fabrice Bellard’s PI page 。
其他计算圆周率的公式包括:
(拉马努金 Ramanujan)
(David Chudnovsky 及 Gregory Chudnovsky)
编写电脑程式时,也可以利用反三角函数直接定义 π 值,但是编译器必须具备三角函数的函式库:
利用正弦函数
利用余弦函数
维基百科关于祖冲之:
祖冲之(429年-500年),字文远,南北朝时期数学家、天文学家。
祖冲之祖籍范阳郡遒县(今河北涞水),为避战乱,祖冲之的祖父祖昌由河北迁至江南。祖昌曾任刘宋的“大匠卿”,掌管土木工程;祖冲之的父亲也在朝中做官。
祖冲之生于建康(今江苏南京)。祖家历代都对天文历法素有研究,祖冲之从小就有机会接触天文、数学知识。祖冲之青年时,就得到博学多才的名声,宋孝武帝听说后,派他到“华林学省”做研究工作。461年,他在南徐州(今江苏镇江)刺史府里从事,先后任南徐州从事史、公府参军。公元464年他调至娄县(今江苏昆山东北)任县令。在此期间他编制了《大明历》,计算了圆周率。宋朝末年,祖冲之回到建康任谒者仆射,此后直到宋灭亡一段时间后,他花了较大精力来研究机械制造。494年到498年之间,他在南齐朝廷担任长水校尉一职,受四品俸禄。鉴于当时战火连绵,他写有《安边论》一文,建议朝廷开垦荒地,发展农业,安定民生,巩固国防。祖冲之在他72岁时去世。
祖冲之的主要成就在数学、天文历法和机械制造三个领域。此外历史记载祖冲之精通音律,擅长下棋,还写有小说《述异记》。祖冲之著述很多,但大多都已失传。
祖冲之的儿子祖暅之也是数学家。
为纪念祖冲之,人们将月球背面的一座环形山命名为“祖冲之环形山”,将小行星1888命名为“祖冲之小行星”,上海浦东张江高科技园区内有一条城市道路命名为“祖冲之路”。
×××××××××××××郁闷的分割线×××××××××××××××××××
今天IE8下面Gmail出现了一些问题,版面混乱,不知道大家有没有出现这种情况:
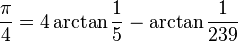
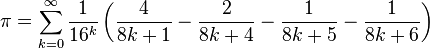
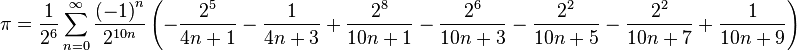
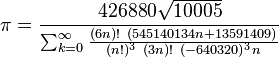

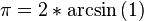




今天上数学课了。我虽然升级了IE8,可是不怎么用。前几天卸载回到Ie6了,帮不到你。
关于Gmail的问题,现在发现并不是Google的问题,而是新升级的IE8出了问题,不光是Gmail,Google Reader以及其他的好几个网站都乱了……
哈~~~
最近忙着考试郁闷去了
现在回来了呢
真的是很久没更新了
中国古人真牛啊
老子很牛叉,后代不争气。
@济南房子网
还好,我没有把自己常用的电脑升级到IE8,哈哈!!降级吧!
完全看不懂计算过程··
@Eden IE6?我现在办公电脑必须要用IE6,郁闷死我了……
@小落 春天怎么会有考试呢?考什么呀?
@仁心博客 对呀,牛一点才有市场嘛
@石老人 好歹我们也是文明古国呀,唉!
@Alex 我抛弃IE,使用chrome了
@贝壳 其实,我也看不懂,就只知道3.1415926
如果不是来你这里,我也确实不知道这个是用来纪念祖冲之的,哈哈。
IE8我还是放弃用了,问题太多了,还是用回FX了。
长江前浪压后浪,古人很牛了,看来还是教育制度的问题 O(∩_∩)O~
看不懂,不过感觉Google创意不错
我尻,这些数字和符号看的脑壳晕啊~~
有时我用IE8登陆Gmail也会出现这样的情况,我当时还以为是网速的原因!不知是否是这样?
对了,我从google reader点击来后,在你的顶端看到“感谢你通过 Google 订阅我”很神奇啊,牛叉!
好啊,就是看不懂!
我就不升IE8,
不是不想,是不敢~哎~
这不能怨Google的,谁知道当年祖冲之用啥表示的圆周率
@ev.code.p 我现在都回到IE6了……
@减肥食谱 其实现在的人也很牛,只不过我们缺少发现牛人的机制
@大帝007 这个主题确实很牛的,很多人的这个提示都会是“通过Google来到这里,为什么不订阅我呢?”其实,我就是用Google Reader过去的。当然,主题不是我做的,我也不知道怎么设置。
@Mr.Chou 有什么不敢的呀,其实电脑就是试验田嘛,想怎么玩就怎么玩。
@游魂 或许用某个象形符号吧……
他们都很牛,我在现代也证不出来
主题漂亮的很
了解
礼尚往来,互相帮助,共同进步。
严重支持
中国人是好牛